
Zadanie Zachody Słońca (zac)
Pomóż nam usprawnić bazę zadań!
Sunsets
Memory limit: 64 MB
Inhabitants of Bytetown love watching sunsets from the roofs of their houses. If a sunset is particularly spectacular, some of them decide to go on the roofs of nearby buildings, so that they have a better view.
Buildings in Bytetown capital are arranged on a grid 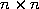 .
Distance between two points is measured using the Manhattan metric.
.
Distance between two points is measured using the Manhattan metric.
John plans to buy a new flat.
He is a great admirer of sunsets and he is ready to walk to some other building
every day to see this inimitable phenomenon.
He would not like, however, to walk further than 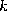 units away from his flat.
units away from his flat.
Help John decide where to buy his new flat.
For a given plan of the city with heights of all buildings specified,
construct a new map, which for each building  specifies the height
of the highest building that John can walk to, assuming that he buys a flat in building
specifies the height
of the highest building that John can walk to, assuming that he buys a flat in building  .
.
Task
Write a program which:
- reads from the standard input the plan of the city with heights of all buildings specified,
- for each building calculates the height of the highest building located not further than
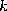 units away from it,
units away from it,
- writes the modified map with calculated heights to the standard output.
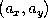 and
and 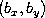 is
is
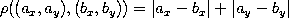
Input
In the first line of the standard input there are two integers  and
and 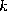 (
(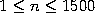 ,
, 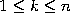 ),
separated by a single space.
In each of the following
),
separated by a single space.
In each of the following  lines there are
lines there are  non-negative integers not grater than
non-negative integers not grater than 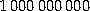 ,
separated by single spaces - they describe the plan of Bytetown.
,
separated by single spaces - they describe the plan of Bytetown.
Output
In each of  lines of standard output there should be
lines of standard output there should be  non-negative integers, separated by single spaces
and describing the modified plan of Bytetown.
non-negative integers, separated by single spaces
and describing the modified plan of Bytetown.
Example
For the input data:
4 2 1 3 4 5 0 2 2 3 4 1 1 3 6 2 3 0
the correct result is:
4 5 5 5 6 4 5 5 6 6 4 5 6 6 6 3
Task author: Krzysztof Duleba.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English